摘要:风险分析是通过对不确定事件的识别、衡量和处理,以最小的成本将各种不确定因素引起的损失减少到最低的科学管理办法。论文以风险理论为指导,初步探讨了粮食生产中的风险问题,并从粮食产量序列入手采用解析概率密度曲线积分的方法,着重研究某一粮食生产单元粮食产量序列的波动情况,定量地反映该地区粮食生产风险水平的高低状况,为发展生产、防灾减灾提供参考。
关键词:风险分析;相对气象产量;概率
中图分类号:X820.4;F307.11
文献标识码:A
文章编号:1000-3037(2001)03-0221-06
1 前言
粮食生产风险研究是适应市场经济发展的农业气象灾害领域中的一个前沿性的课题。农业灾害具有二重性:即灾害的自然属性和灾害的社会属性。农业灾害的自然属性主要是指致灾因子如洪涝、干旱、冰雹、冷害等危害农作物生长发育和产量形成,破坏农业基础设施甚至造成人员伤亡等后果,包括可感觉得到的一次、二次以及有因果关系的两重性连锁影响。当这些影响与公众期待的状况出现难以接受的差距时,就上升为社会问题了[1]。因此,粮食生产同时具有自然风险和社会风险。
2 粮食生产中的风险问题
粮食生产风险分析是通过对农作物生长期内(甚至非生育期)可能遭遇到的不确定事件的识别、衡量和处理,以最小的成本将各种不利后果减少到最低程度的科学管理技术。基本内容包括风险辩识、风险估计和风险评价三部分[1、2]。其含义和关系可由下面的模型表示 ( 图 1)。
 |
图 1 粮食生产风险分析内容
Fig.1 Content of grain yield risk analysis
2.1 风险辨识
风险辨识是对面临的潜在风险加以判断、归类和鉴定风险性质的过程。对粮食生产风险来说,要求回答以下几个问题:
(1) 应该考虑哪些风险事件?风险事件是风险辨识的起点,按照作物对不良条件反馈滞后时间的长短不同,可将风险事件分为慢性发作型风险事件和急性发作型风险事件。前种风险事件在植株受到危害时往往没有明显的生理和病理反应,只有当不利条件对新陈代谢、生长发育的抑制作用和对植株的损伤累积到相当程度时才会对产量造成较大的影响;后一种风险事件是当致灾因子程度剧烈,超过了受灾农作物的适应能力而使植株发生明显的病理变化或器官损伤,如茎秆折断、叶片卷曲、落花落果、倒伏等。与此类似,按照不同分类方法可以划分不同性质的风险事件。
(2) 引起风险事件的原因是什么?致灾因子和孕灾环境是引发风险事件的深层次原因。例如,植株叶片枯萎,可能是由于干旱、冻害、霜冻、热害、病虫害等原因引起,而对干旱来说久旱不雨、大气蒸发过于旺盛、土壤中有毒物质的积累是更进一步的原因。探讨风险事件的原因应与及时、广泛的大面积田间调查相结合;把损失资料与各种致灾因子资料相结合,利用数理统计和模拟的办法可以定量地研究风险事件的起因。
(3) 风险事件引起的后果及严重程度如何?风险事件发生后使农作物减产是众多不利影响中最重要的部分,此外还会对社会生产、生活造成更深远的作用。
2.2 风险估计
风险估计是在风险辨识的基础上,给出某一风险事件发生的概率及其后果,一般采用概率树的方法可以直观地表示出来[3]。但是,农作物的全生育期可能遭受一系列致灾因子的作用,而且这种作用是非线性形的,难以分离出单一致灾因子的危害后果,故概率树方法的实现有一定的困难。理论概率分布是另一种风险估计的方法。对给定生产单元的产量序列,通过一定的变换,利用解析概率密度曲线方法可以计算出任意增产率区间和减产率区间的风险水平。
2.3 风险评价与决策
风险评价与决策的内容是在了解粮食生产中已知风险事件的风险水平的基础上,判断是否采取措施,采取什么措施,以及采取措施后可能出现什么后果等作出决定,过程见图 2。
 |
图 2 风险评价与决策过程
Fig.2 Process of risk analysis and decision making
风险评价与决策的方法主要有如下几种[1~4]:
(1)回避风险方法:包括采用各种防灾、抗灾措施,抗御不利气象条件对作物的危害,增强植株抗逆性、改良局地生态环境、灾后补救等;或者在种植某作物高风险区改种其它风险较小的作物。
(2)权衡风险的方法:在一块面积广大的农业种植区,风险水平存在差别。针对局部区域风险水平的差异采取不同的农业技术措施,如作物布局、耕作方法、管理方法等可以减少灾害的不利影响。
(3)风险评价的综合分析方法:在相同的风险区内,最优的农作物布局可以使粮食产量的波动最小,综合经济效益最佳。借助于系统规划这一数学工具,考虑品种搭配、种植面积、播种日期、农业投入等因子可以实现这一目标。
(4)保险转移:在生产条件恶劣、产量不稳的地区或者为追求较高的经济效益而面临高风险的农民应该借助于保险的方式转嫁高风险,确保最佳的经济效益和生产、生活的稳定。由农民向保险公司投保,以交纳保险费为代价将风险转嫁给保险公司,一旦作物遭受损失可由保险公司予以补偿。
3 解析概率密度曲线法估计粮食产量序列的风险概率
由图 1 和以上风险分析的内容可知,在粮食生产风险分析中,风险估计不仅可以直观给出粮食产量风险水平的高低状况,而且是风险评价与决策的基础,因而占据非常重要的地位。本文拟采用概率统计的方法,其实质是分布函数及特征参数的计算,将粮食产量序列处理后以某一概率密度函数表示出来,根据概率密度函数的统计性质计算风险水平,为风险决策提供依据。
对于一个粮食产量序列而言,总体来看,多年来基本呈上升的趋势,可以看作是不同尺度波动的叠加结果。我们关心的是年际尺度的产量的波动状况,为合理反映这一信息,必须对产量资料进行处理,从中解析出产量波动的年际变化信息,为估计风险水平做准备。
3.1 粮食单产分解
粮食产量资料来自中国统计部门,序列长度为 40 年以上(1949~1996 年 48 年的资料)。影响粮食产量形成的各种自然和非自然因素可以按影响的性质和时间尺度划分为农业技术措施、气象条件和“随机噪声”三大类,其中“随机噪声”类比较小,可忽略不记。与此对应,粮食产量序列分解为两个周期不同的波动的合成 [5]
Y=Yt+Yw (1)
其中,Y 为粮食单产,Yt 是反映历史时期生产力发展水平的长周期产量分量,称为趋势产量;Yw 是受以气象要素为主,包括市场价格、政治因素在内的短周期变化因子影响的产量分量,称为气象产量,以一年为周期。本文采用正交多项式逼近的方法求出趋势产量 Yt( 多项式取 9 项 ),则气象产量
Yw=Y-Yt (2)
进一步作相对化变换
X=Yw/Yt (3)
此时,气象产量就变成一个相对比值,不受历史时期不同农业技术水平的影响,称为相对气象产量。其物理意义表明粮食波动的幅值,不受时间和空间影响,具有可比性,能较好地描述以气象要素为主的各种短期变动的因子对产量序列的影响。由于相对气象产量是一个比值,表明实际粮食单产偏离趋势产量的波动幅值,为研究方便,本文作如下定义:实际单产低于当时趋势产量的百分率称为“减产率”(相对气象产量百分率为负值);高于趋势产量的百分率称为“增产率”(即相对气象产量百分比为正值)。图 3 为河北省粮食相对气象产量序列图。从图中可以看到,产量序列在 60 年代初有较大的减产,这与当时的社会历史背景和自然条件有关;还可看到,产量波动幅度 80 年代以后比 80 年代以前小,这是由于生产条件的改善和土地承包后,农民积极性提高,从而使粮食产量稳步增长。另外,进入 80 年代以后,中国洪涝灾害的高发区由黄淮海地区转移到长江中下游地区,也使河北粮食产量波动减少。
3.2 解析概率密度曲线积分法估算风险概率
计算风险水平有很多方法,本文采用一种通用的构造概率密度函数的方法,对任意一个相对气象产量序列首先构造概率密度函数,根据概率密度曲线估计风险水平。具体分以下几个步骤进行。
3.2.1 用近似解析式表示相对气象产量序列的概率密度曲线
在相当长的一段时间内,由于每年的气象条件、农业生产措施等不同,造成粮食产量的不确定性,使相对气象产量序列具有随机变量序列的特点(图 3),其数值一般介于-1 和 1 之间。为研究该随机序列的特性,本文采用近似解析式来构造相对气象产量序列的概率密度函数,将看似无序的相对气象产量序列的性状表示出来。
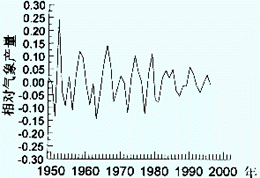 |
图 3 河北省相对气象产量序列图
Fig.3 Relative meteorological yield sequence of Hebei
令 f(x) 是相对气象产量序列的概率密度函数的解析式形式[6]:
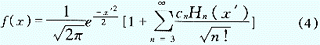 |
其中 ,x ′为正规化的相对气象产量;Hn(x ′) 为艾尔米特多项式,可表示为:
 |
系数 cn 与概率密度 f(x) 所表征的相对气象产量序列 x 的 k 阶矩有关,本文以河北省粮食产量序列 x ′为例,系数取前 6 项,分别为 c1=0.0,c2=0.0,c3=0.10962,c4=0.354102,c5=0.3230497,c6=-0.658931;为正规化的相对气象产量序列。利用 (4) 式只需要不多几项就可精确地表示相对气象产量这种随机变量的的概率密度函数。
根据式 (4),以河北省为例,拟合得到河北省粮食产量序列概率密度曲线。如图 4 所示,该曲线描述了相对气象产量序列的分布特点。从该曲线可以看到,相对气象产量的增减产概率主要集中于-0.3~0.3 之间,尤其是-0.1~0.1 内,表明该省粮食产量历年来增长稳定,出现大丰收年和大减产年的概率较少。将图 3 与图 4 比较发现,图 3 显示的相对气象产量数值基本在-0.2~0.25 之间,与图 4 十分接近,但图 4 的曲线不仅可以显示出已知相对气象产量的增减产信息,对潜在的相对气象产量的可能范围也作出界定,图 4 包含的信息多于图 3。由于本文所用粮食产量资料样本数较大 ( 近 50 年 ), 达到了农业气象研究中大样本的要求 (30 年 )[7], 可以认为,该序列具有代表性,因而利用粮食产量资料构造的概率密度函数可以反映该省多年来粮食生产风险水平状况。通过该函数,可以将研究离散的相对气象产量序列的性质转化为对连续性随机变量的研究,不但可以得到已有数据的统计性质,还可以推断一般增产率区间或减产率区间的性质。
 |
图 4 河北省粮食产量序列概率密度曲线
Fig.4 Probability curve of Hebei
3.2.2 高斯求积法计算分布函数
相对气象产量序列的概率密度曲线 f(x) 虽然从离散点构造而来,但当把 x 视为连续型随机变量时,该概率密度函数则变为描述连续型随机变量的概率密度函数。为研究在不同增产率区间和减产率区间的风险概率,需要从概率密度曲线求取分布函数,由分布函数可以获得某一风险水平的风险概率。
相应于相对气象产量序列的概率密度函数 f(x),其分布函数为:
 |
显然,对分布函数的计算可以归结为积分的计算,上式中 x 为相对气象产量。
由于高斯求积法是具有最高代数精度的求积公式[8],故本文采用此法计算相对气象产量序列概率密度曲线的分布函数。对相对气象产量序列的概率密度曲线积分,得
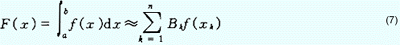 |
如果结点 xk 不固定,把它看成 n 个可自由选择的参数,则上式右端有 2n 个 Bk 和 xk 待定参数,那么该公式就可能对 2n-1 次多项式精确,如何确定系数 Bk 及结点 xk,使上式代数精度达到 2n-1,这就是构造高斯高精度求积公式的基本思路。
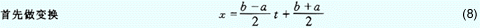 |
将原积分化为在区间[-1,1]上的积分,即:
 |
 |
 |
如果 n 个插值结点取勒让德(Legendre)多项式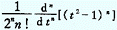
在区间[-1,1]上的 n 个零点,则插值求积公式称为高斯求积公式,其代数精确度为 2n-1。本文取 n=5。
分布函数为非降函数,在任意一点上,表示相对气象产量小于该点的情形,但为了直观表示相对气象产量实际增减产幅度,本文所求的概率密度曲线以相对气象产量的可能变化范围作为 x 轴 ( 而不是以正规化的相对气象产量为 x 轴 ),故概率密度曲线所围面积不等于 1,因此直接对任意增减产范围积分并不能表示风险概率,尚需做相对化处理。
3.2.3 计算任意增产率区间或减产率区间的风险概率
由图 4 可见,对任意相对气象产量序列,标示所有可能生产状况可以用分布函数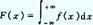 来表示。对某种生产状况,如粮食生产增产率或减产率介于 a 与 b 之间可以用积分
来表示。对某种生产状况,如粮食生产增产率或减产率介于 a 与 b 之间可以用积分 来表示。则介于 a 与 b 之间的风险概率就是概率密度函数在 a 与 b 之间围成的面积
来表示。则介于 a 与 b 之间的风险概率就是概率密度函数在 a 与 b 之间围成的面积 与概率密度函数在-∞~+∞间所围面积之比
与概率密度函数在-∞~+∞间所围面积之比
 |
以北京市和河北省为例,采用上述方法计算不同风险水平的风险概率,结果如表 1 所示。
表 1 北京市、河北省粮食产量风险水平计算结果 (%)
Table 1 Results of risk probabilities of Beijing and Hebei
| 增产率区间和 减产率区间 |
-30%~ -20% |
-20%~ -10% |
-10%~ -5% |
-5%~ 0% |
0%~ 5% |
5%~ 10% |
10%~ 20% |
20%~ 30% |
|---|---|---|---|---|---|---|---|---|
| 北京市 | 1.6 | 13.5 | 13.4 | 19.7 | 23.2 | 17.2 | 6.7 | 1.8 |
| 河北省 | 0.4 | 9.2 | 16.6 | 25.5 | 24.2 | 14.2 | 8.8 | 1.0 |
从而说明:①由表 1 发现,北京市和河北省粮食产量年际波动幅度近 50 年来大部分界于-20%~20% 之间,出现概率分别达到 96.6% 和 98.5%;尤其是出现在-10%~10% 之间的概率分别达到 76.4% 和 80.5%;而粮食产量减产率低于-30% 和增产率高于 30% 的全部可能性,北京市略高于河北省,这是由于河北省面积广大,平均单位产量较北京波动更小。尤其是 80 年代以后,由于生产力的发展和天气条件等短期变化的风险因子波动较小,产量年际波动幅度变小,粮食生产面临的风险较小;②利用解析概率密度曲线法构造粮食产量序列的概率密度函数对样本数本身没有要求,但若希望构造的概率密度函数能代表该生产单元多年总的风险水平状况,则样本数 N 至少大于 30 以满足大样本量的要求。样本量越大越,接近整体,计算的结果越符合实际情况;③利用解析概率密度曲线法估计粮食生产风险水平时,粮食产量序列分解的合理性最为关键,作者曾采用正交多项式逼近法、直线滑动平均法和分段模拟方法,发现前两种方法得到的结果比较接近。如何将粮食产量序列最佳地分解为年际变化的分量和长周期分量,是今后亟待改进的地方;④目前有关部门进行农业产量预报时均只预报某一具体数值,该值只是未来年份粮食产量概率空间多种可能性中的一个。如在进行产量预报时,结合本文风险估计的结果并采用计算机仿真的方法,则可以得到未来年份粮食产量的概率预报。
4 结语
以风险理论为指导,初步探讨了粮食生产中的风险问题:利用风险辨识方法及早发现农作物生长发育过程中的风险事件,追溯风险源,以便对粮食生产中的风险问题有一个全面深入的了解;对某一生产单元多年粮食单产风险水平高低进行了数值计算,结果反映了该生产单元粮食产量年际变化幅度的大小和在不同增产率和减产率期望下面临的风险水平。风险估计的结果是风险决策的基础。在粮食生产的风险评价与决策方法中提出了自己的一些想法,包括回避、抗御、规划等方法。本文将重点放在风险理论的核心部分——即风险估计上。由于农作物在全生育期会遭遇很多风险事件,但风险事件的最终影响均体现在粮食产量上,所以,对粮食产量进行风险分析有现实意义。所采用的解析概率密度曲线积分法是基于笔者对风险理论的理解综合国内外一些研究成果独立提出的方法,通过与其它方法对比,表明此法有更高的精度。根据风险估计的结果可以评价不同地区粮食产量的稳定性状况;结合计算机仿真方法可对将来的粮食产量进行概率预测;为农作物保险时计算保险费率和农民交纳保险金提供依据;可以评价地方上报粮食产量数据的可靠性,为决策部门防灾减灾提供依据。
参考文献

|
高中各年级课程推荐
|
||||
|
年级
|
学期
|
课程名称
|
课程试听
|
|
| 高一 |
高一(上)、(下)同步复习
|
语文 | ||
| 英语 | ||||
| 数学 | ||||
| 数学(期中串讲) | ||||
| 数学(期末串讲) | ||||
| 数学拔高 | ||||
| 物理 | ||||
| 化学 | ||||
| 生物(一) | ||||
| 地理 | ||||
| 历史 | ||||
| 政治 | ||||
|
高中专项突破课
|
语文写作 | |||
| 英语阅读理解 | ||||
| 英语写作 | ||||
| 英语完形填空 | ||||
| 物理功和能量 | ||||
| 高二 |
高二(上)、(下)同步复习
|
语文 | ||
| 英语 | ||||
| 数学(理) | ||||
| 数学拔高(理) | ||||
| 数学(文) | ||||
| 数学拔高(文) | ||||
| 物理 | ||||
| 数学(期中串讲) | ||||
| 数学(期末串讲)(理) | ||||
| 数学(期末串讲)(文) | ||||
| 化学 | ||||
| 生物(一) | ||||
| 生物(二) | ||||
| 生物(三) | ||||
| 地理 | ||||
| 历史 | ||||
| 政治 | ||||
| 高三 |
高考第一轮复习
|
语文 | ||
| 英语 | ||||
| 数学(理) | ||||
| 数学拔高(理) | ||||
| 数学(文) | ||||
| 数学拔高(文) | ||||
| 物理 | ||||
| 物理拔高 | ||||
| 化学 | ||||
| 生物 | ||||
| 地理 | ||||
| 政治 | ||||
| 历史(韩校版) | ||||
| 历史(李晓风版) | ||||
|
高考第二轮复习
|
数学(理) | |||
| 数学(文) | ||||
| 英语 | ||||
| 物理 | ||||
| 化学 | ||||
| 地理 | ||||
|
高考第三轮冲刺串讲
|
语数英串讲(理) | |||
| 语数英串讲(文) | ||||
| 物化生串讲 | ||||
| 史地政串讲 | ||||
|
高考试题精讲
|
数学(理) | |||
| 英语 | ||||
| 化学 | ||||
| 物理 | ||||
| 2021高考研究2021高考策略(理) | ||||
| 2021高考研究2021高考策略(文) | ||||
Copyright © 2005-2020 Ttshopping.Net. All Rights Reserved . |
云南省公安厅:53010303502006 滇ICP备16003680号-9
本网大部分资源来源于会员上传,除本网组织的资源外,版权归原作者所有,如有侵犯版权,请立刻和本网联系并提供证据,本网将在三个工作日内改正。

